The significant rise in temperature during the past decades is not the only sign of climate change. There are many other climate indices that illustrate the changes to the climate. The change in key parameters over time is shown here.
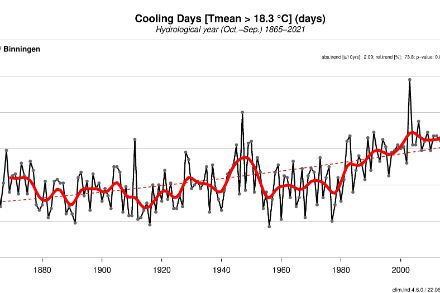
A number of climate indices clearly show how Switzerland is affected by climate change. For example, the observed warming also means that the number of summer days and hot days is increasing (daily maximum temperature 25°C or 30°C or more, respectively), as is the number of tropical nights (lowest temperature not below 20°C). At the same time, the number of frost and ice days (minimum or maximum temperature below 0°C) is decreasing.
Another result of warming is a decrease in the number of fresh snow days and days with snow cover, despite a trend towards higher levels of winter precipitation. Since the 1980s, there has also been a trend towards more sunshine and clear days. Whether a climate index shows any statistically verifiable trend, and how strong that trend is, depends on the location and the observation period.
Climate indices are available for most of the stations in the Swiss National Basic Climatological Network. They are calculated using homogenised data for the normal periods from 1864 to date and 1961 to date, where these data exist. Climate data are homogenised when they are adjusted to take account of any influences that are not associated with climate or climate change. This would be the case, for example, if the conditions under which meteorological data are collected have changed. No homogeneous series are available as yet for snow or for indices that are based on sunshine duration; these are evaluated from the original data, which is checked and adjusted.
The application below will display climate indices for heat, cold, rain, snow, drought and sunshine.
Trends are determined as follows:
Various drought indices are used to describe the current levels of drought or wetness at selected stations in the MeteoSwiss monitoring network. The indices are derived from meteorological parameters. The most important input variable is the precipitation amount. With certain indices, evaporation is also taken into account, which is dependent on temperature, humidity, radiation and wind speed.
The following literature sources were used: