Service Navigation
Search
Wind is generated due to a difference in pressure (pressure gradient) between two points, when the air particles are forced to move from the area with higher pressure (high-pressure area) towards the area of lower pressure (low-pressure area).
It would be reasonable to assume that, after the formation of a low-pressure area, a rapid compensatory flow would occur and the low-pressure area would be "filled up" by the neighbouring high-pressure areas. This is not the case, however, because unlike a ball rolling straight down a hill, winds circle around a low-pressure area, and the process of filling takes a very long time. So, why doesn't the air flow directly from the high-pressure area to the low-pressure area? The reason for this is the Coriolis force, which deflects the winds to the right in the Northern Hemisphere and to the left in the Southern Hemisphere.
We can do a small experiment to illustrate the Coriolis force: Take a sheet of paper and a pen. First of all, draw a straight line from the bottom of the page to the top. Now do the same again, starting at the same point but rotating the paper anticlockwise while drawing. This time, the line is not straight but curved, even though you aimed for the same endpoint.
In physics, any curved trajectory must be caused by a force, so the concept of the Coriolis force was introduced to mathematically describe the processes in rotating systems. This is not a "real" force, like the gravitational force between the Earth and a stone, for example, but rather an apparent force because it is dependent on the frame of reference.
On Earth (a rotating system), the Coriolis force acts (as in the experiment described above) on an air parcel moving in a straight line, such as from the equator to the North Pole. If we were to observe the trajectory from outside the Earth (e.g. from above the North Pole), the path would appear straight. However, if we are on Earth, the trajectory is curved to the right.
The Coriolis force affects everything that moves on Earth, including water in the oceans and droplets in the atmosphere. It acts perpendicular to the direction of movement and is proportional to the speed of movement, but its intensity varies with latitude. The Coriolis force can deflect the trajectory of a moving object, but it has no direct impact on the object's speed.

Relationship between the Coriolis force and latitude
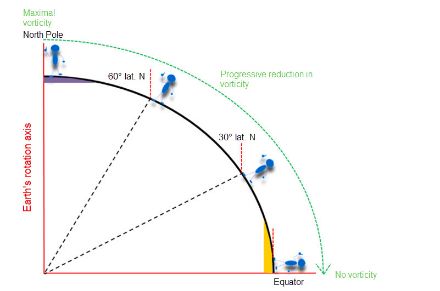
As described above, the Coriolis force is closely linked to the Earth's rotational movement around its axis. However, the impact of this movement on the Coriolis force depends on the latitude; it is zero at the equator and at its maximum at the poles.
Let's illustrate this with an example: Imagine you are standing in the middle of a fairground carousel. It is rotating on its axis, and at the same time, it is rotating you on your own axis. Your body gains a certain rotational motion from the carousel, which in meteorology is referred to as vorticity.
This vorticity remains constant regardless of whether you are at the centre of the carousel or moving towards the edge. Wherever you are positioned, you will complete a full rotation in the same amount of time (the axis of the carousel runs parallel to the vertical axis of the person on the carousel). What changes is the speed of the movement around the axis, which increases as you move further away from the axis.
The Earth, however, is not a carousel (i.e. a disc) but a sphere, which makes a significant difference. If you stand at one of the poles, the Earth's rotational axis is exactly parallel to your body's axis (like on the carousel). In this case, the Earth's rotation causes you to rotate with it around your own axis. But if you take a journey from the pole to the equator, your body's axis will gradually move away from the direction of the Earth's rotational axis until, at the equator, it is standing exactly perpendicular to it. At this point, the vorticity of your body is zero. This is because, at the equator, the Earth's rotation causes you to move around the globe, but you do not have any rotation around your own axis. In other words, the further you move away from the poles, the faster you rotate around the Earth's axis, but the less you rotate around yourself. So, what does this mean in relation to air masses? The same rules actually apply here, too.
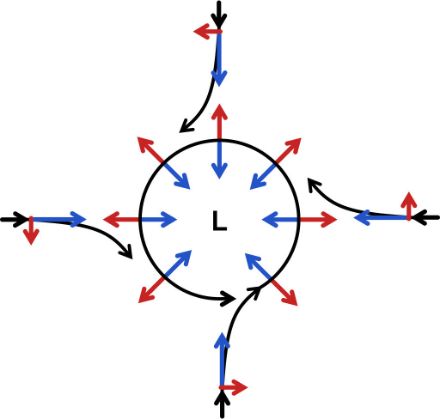
A specific example for the Northern Hemisphere
The diagram below shows the trajectory of air parcels moving in the Northern Hemisphere from the four cardinal directions. The blue arrows represent the pressure gradient force, the red arrows the Coriolis force, and the black arrows the actual trajectory of the air parcels. Before an air parcel starts moving, only the pressure gradient force acts on it, pushing the air from high to low pressure. As soon as the air parcel begins to move, the Coriolis force starts to act on it, provided it is not too close to the equator. This force acts perpendicular to the movement, deflecting the air parcel to the right (red arrows). The Coriolis force increases as the speed of movement increases, and this causes the air mass to deflect further to the right, while the pressure gradient force remains constant and is always directed towards the centre of the low-pressure area. At the point of equilibrium, the two forces act in opposite directions and are of equal magnitude. At this point, the wind flows parallel to the isobars (lines of equal pressure). This wind, which is more theoretical than real, is known as the geostrophic wind. If conditions remain unchanged, this equilibrium point can remain in place indefinitely. However, other forces also act on the air parcel – especially friction, at lower altitudes – and eventually cause the low-pressure areas to fill again.
This tells us that the Coriolis force is only noticeable in large-scale phenomena and that it takes some time for its full effect to become apparent. In more localised phenomena, such as the Föhn or Joran winds, its effect is negligible, and therefore not perceptible. The Coriolis force is equally negligible when it comes to water draining down the plughole in a bathtub. In contrast, it has a very clear and direct influence on the westerly flows of the mid-latitudes and the tropical trade winds.